Tower of Hanoi

The Tower of Hanoi is a puzzle using three rods and an n number of disks. Each of these disks have a different diameter and can fit on any rod. At first, all of the rods are stacked on the first rod in order of size, with the largest disk on the bottom and the smallest on top. The goal is to move the stack to the third rod under the following rules: only one disk can be moved at a time, a disk can only be taken from the top of one stack and put on the top of another, and no disk can be placed on a smaller disk.

The puzzle was made by Édouard Lucas in 1883, but it is arguably more famous in its form as “The Tower of Brahma”, with 64 disks. The myth is that the universe will end when the 64-disk puzzle is completed. In reality, it would take about 585 billion years to complete with one move per second.

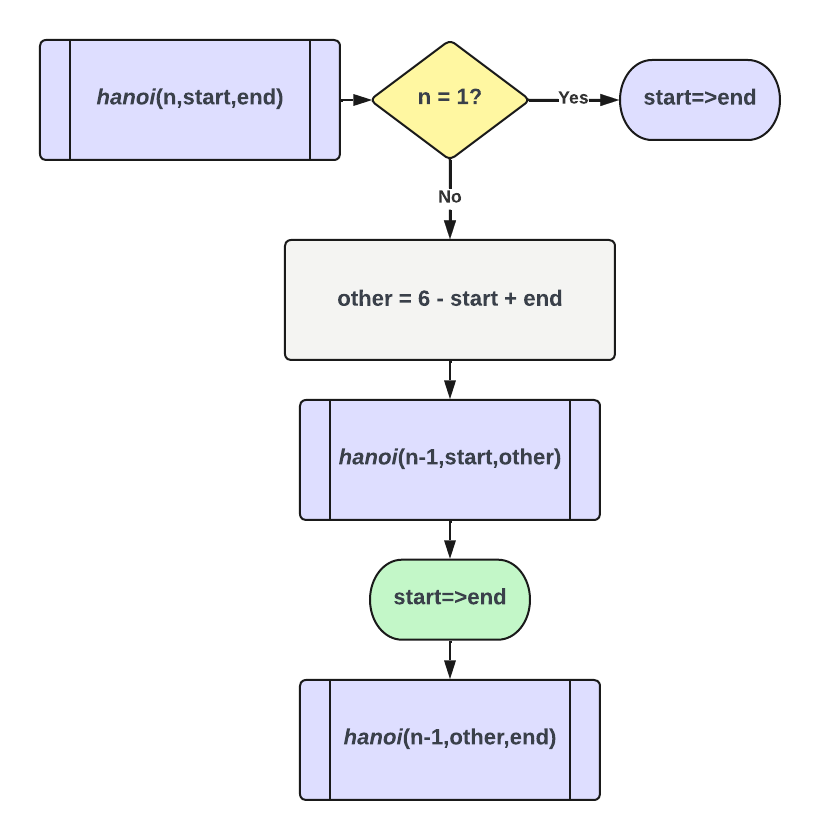
The minimum number of moves needed to complete a Tower of Hanoi puzzle is equal to 2ⁿ-1 where n is the number of disks. The algorithm that my code uses is recursive. It turns the n-disk puzzle from the start rod to the end rod into three steps. The first step is to move a stack of n-1 disks to the third rod, the one that is neither the start nor the end. Then move the n^th disk from the start rod to the end rod. Then move the n-1 stack to the end rod on top of the n^th disk. Since moving the n-1 stack works the same as the n-disk stack, only with the rods and number of disks changed, the process needs to act recursively.

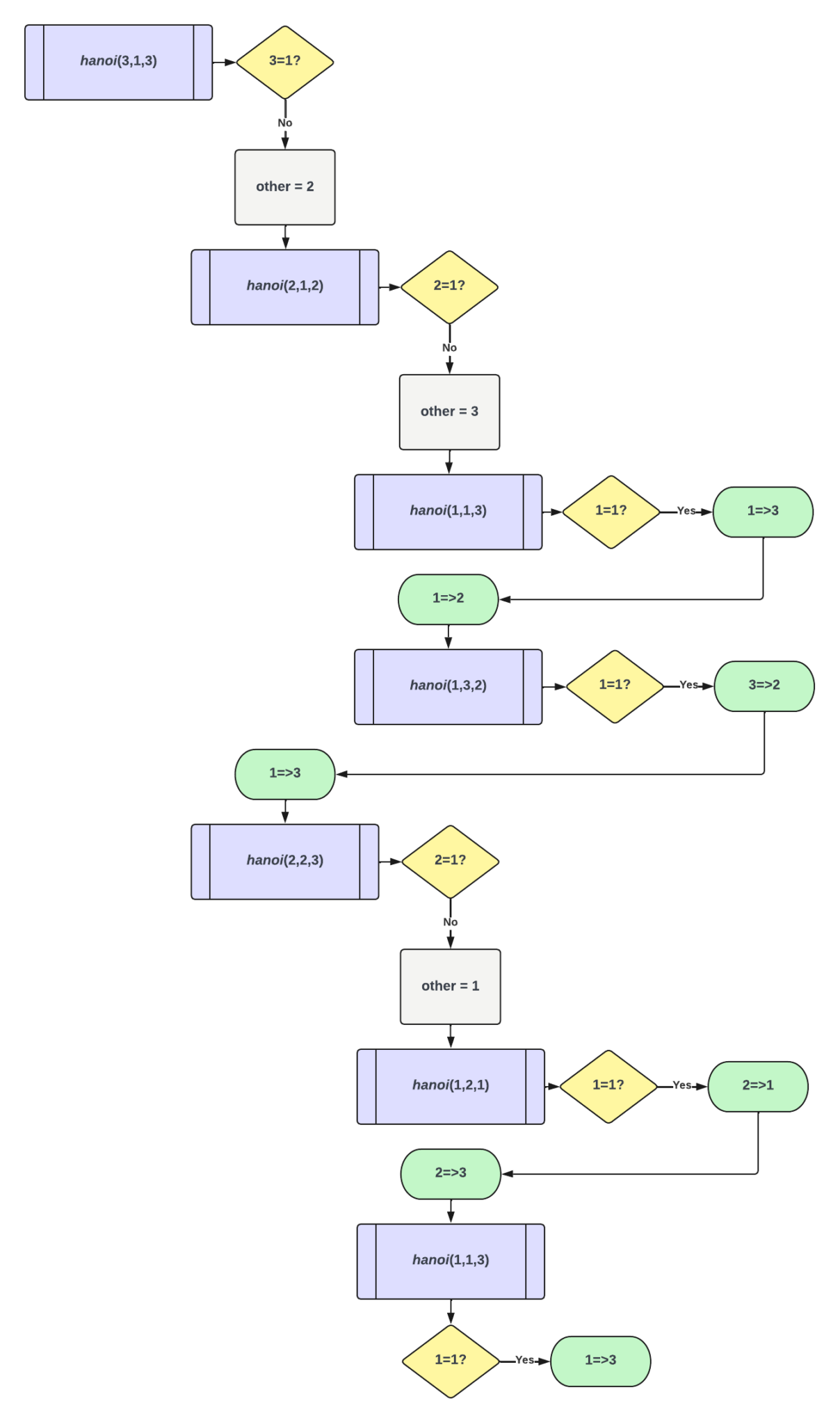
The rods are labeled 1, 2, and 3, going left to right. hanoi takes two of these as the start and end rods. The value of the third rod can be found by subtracting the sum of the start and end rods from 6. Below are two flowcharts for hanoi and hanoi with three disks. Under those are two GIFs of the solutions to the three- and eight-disk puzzles. Here is my Python code.
​

Flowchart of hanoi

​

Flowchart of hanoi with three disks

​

​